Mode coupling
Mode cross coupling of Earth’s free oscillations
Theoretical seismology involves the modelling of synthetic seismograms, for which we are using an expansion in terms of the Earth’s free oscillations. Our work shows that the commonly used self-coupling and group-coupling approximations represent a poor approximation to full-coupling. This result indicates that the more complete full-coupling theory is necessary to retrieve information about density (which can only be obtained from normal modes) in addition to velocity. The relative scaling between perturbations in velocity and density are key to understanding if heterogeneities in the Earth’s mantle and core are caused by thermal variations alone, or if compositional variations are needed as well.
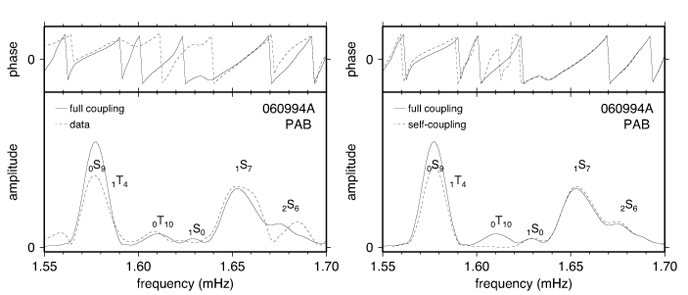
Normal mode spectrum at station PAB for the large and deep Bolivia event of 9 June 1994. The differences between full- and self-coupling synthetics (right) are of the same order as the differences between the observed data and full-coupling synthetics (left) that one would attempt to model (from Deuss & Woodhouse, 2001).
I have spent several years developing and extending this method. I have developed an iteration method which will allow implementation on cluster computers, and studied the importance of full-coupling for attenuation, velocity and anisotropic structure. We also developed a new theoretical formalism to include hemispherical structure in inner core anisotropy in the calculation of fully coupled normal mode spectra. We are now applying our new methods to study the Earth’s mantle and core. Cross-coupling has enabled us to observe hemispherical structure in the Earth’s inner core and make the first observations of the elusive core-mantle boundary Stoneley modes. We have also used normal modes to study the anelastic anisotropy of the inner core.
Reviews
- Woodhouse, J. and Deuss, A. (2015). Theory and Observations – Earth’s Free Oscillations, In Treatise on Geophysics (Second Edition) 1, G Schubert (ed)., Elsevier , p79–115
Publications
- Mäkinen, A. M. and Deuss, A. (2013). Normal mode splitting due to inner core attenuation anisotropy, Geophysical Journal International 195(3) , p1786–1795
- Al-Attar, D., Woodhouse, J. H., and Deuss, A. (2012). Calculation of normal mode spectra in laterally heterogeneous earth models using an iterative direct solution method, Geophysical Journal International 189(2) , p1038–1046
- Koelemeijer, P. J., Deuss, A., and Trampert, J. (2012). Normal mode sensitivity to Earth’s D″ layer and topography on the core-mantle boundary: what we can and cannot see, Geophysical Journal International 190(1) , p553–568
- Deuss, A., Irving, J. C. E., and Woodhouse, J. H. (2010). Regional Variation of Inner Core Anisotropy from Seismic Normal Mode Observations, Science 328(5981) , p1018–1020
- Irving, J. C. E., Deuss, A., and Woodhouse, J. H. (2009). Normal mode coupling due to hemispherical anisotropic structure in Earth’s inner core, Geophysical Journal International 178(2) , p962–975
- Irving, J. C. E., Deuss, A., and Andrews, J. (2008). Wide-band coupling of Earth’s normal modes due to anisotropic inner core structure, Geophysical Journal International 174(3) , p919–929
- Deuss, A. and Woodhouse, J. (2004). Iteration method to determine the eigenvalues and eigenvectors of a target multiplet including full mode coupling, Geophysical Journal International 159(1) , p326–332
- Deuss, A. and Woodhouse, J. (2001). Theoretical free-oscillation spectra: the importance of wide band coupling, Geophysical Journal International 146(3) , p833–842

